Recently I was introduced to PyBites by one of my dear colleagues, and I've decided to solve challenges on a regular basis as a Python refresher. Also as someone who missed Computer Science studies, I was always aiming for better understanding of algorithms - which I know, we don't necessarily use as often as we imagine at our beginning of our career, but lets be honest and appreciate them for transforming our way of thinking and enabling writing code where we at least know how efficient it is and whether it could be more efficient.
I'm planning to cover different algorithms in the frame of a series, and I'd like to start with something I often found hard to grasp and what amazed me at the same time. But let's reveal it through a problem statement - which you might be already familiar with, being popular during coding interviews.
Problem
You are tasked with counting the amount of islands in a 2D matrix / grid.
Islands are represented by 1s, oceans by 0. If the 1s are connected either horizontally or vertically (not diagonally), then they count as one island. You can assume a grid has a limited size up to 10x10. Try to make the search / count of number of islands as efficient as possible. If no islands are found, just return 0.
The goal is to find how many islands there are in the ocean, regardless of its size. [^1]
Consider a visual representation of the given islands and the ocean like this (which later in Pseudo and Python code we will recall as the grid):
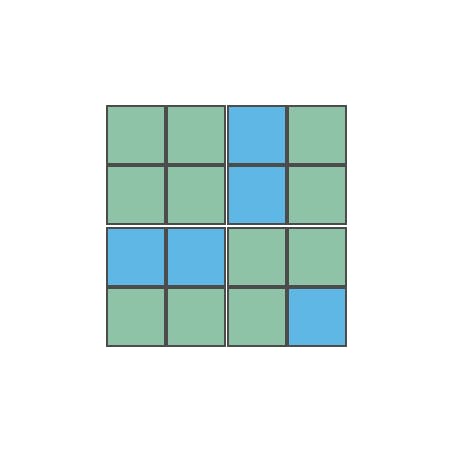
where
- green squares are islands
- blue squares are ocean
The grid itself can be captured as a list of lists:
squares = [[1, 1, 0, 1],
[1, 1, 0, 1],
[0, 0, 1, 1],
[1, 1, 1, 0]]
I used to be horrified about the idea of coding on paper, but what I found good practice is to sit down and think about how I would like to approach and build up my solution - without writing any piece of code just yet. So my solution will become applicable to any programming language - essentially this is what Pseudo code is for. This holds true not only for algorithmic, but any kind of challenges you may encounter during your work, because it only contributes to well-written and structured, more maintainable code if you do so.
Approach
Sticking to this example, the high level idea can be put very simply. We just have to think about the definition of an island, which we all know:
An island is a piece of land surrounded by water on all sides.
💡 We have to go to each (is)land - marked with 1 -, and their nearby (is)lands (referenced from now on as neighbours) on each side (we have 4 of them, according to the problem statement), until there are nowhere to go*, because we either:
- a. ) went back to the land (we've already been to),
- b. ) encountered water, or
- c. ) ran off the grid (bringing in programming perspective and the boundaries of lists)
In other words, what we are planning to do with one item, once we have its neighbours, we are doing the same with them as well. More precisely, what we are doing is
[...] based on the fact that a function can be reused and called within itself to solve a problem that can be broken down into smaller repetitive small incremental and inductive steps in which each one calls the same function with a variation of the original input until a certain condition is satisfied. [^2]
This is by definition, recursion.
That certain condition is often referred to as base case, and its absence can result in all programmers' nightmare, known as infinite recursion.
However, the until there are nowhere to go phase and its implications sounds like a pretty good base case, doesn't it?
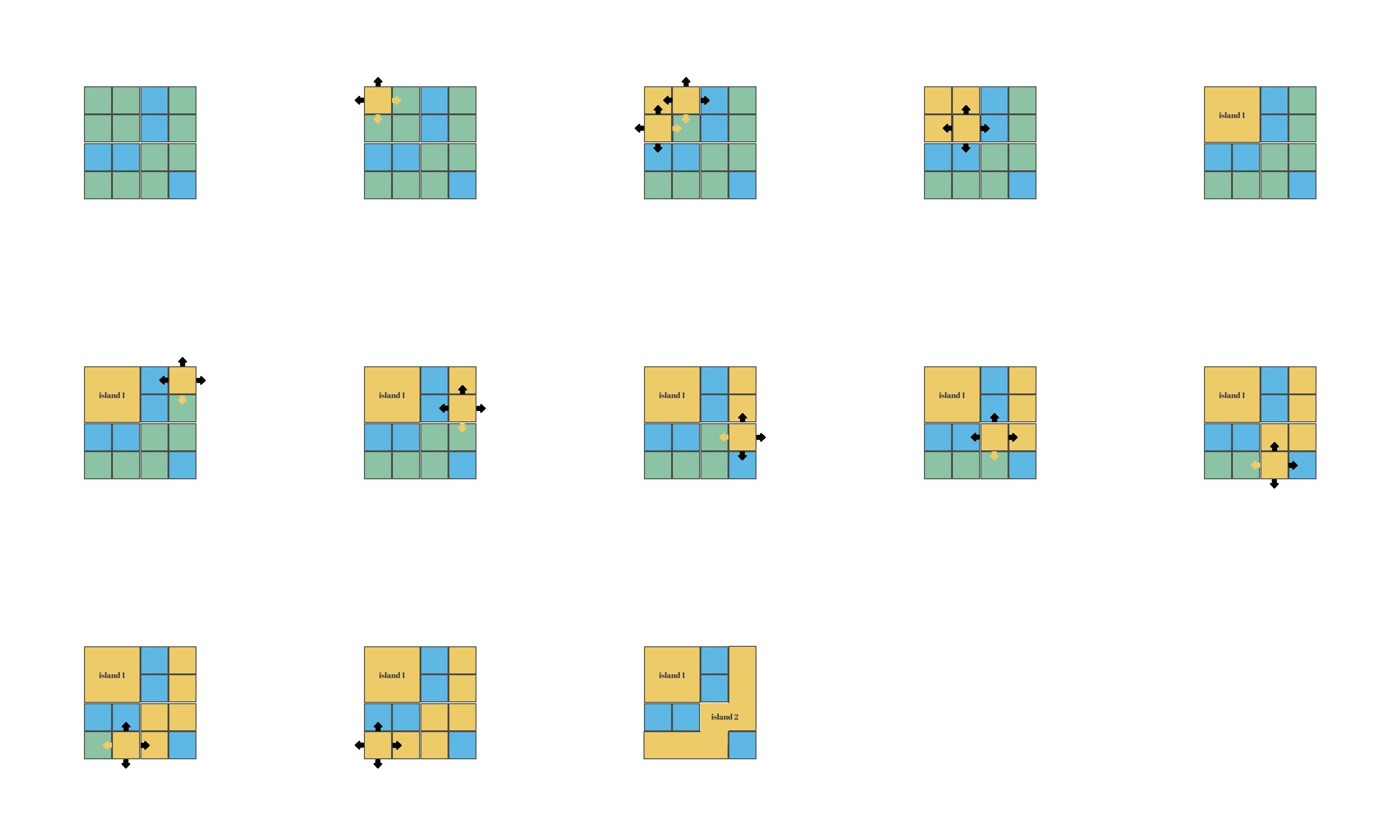
I've put together an animation where you can follow along what is happening step by step:
At this point we are good to go and implement our approach - my choice of programming language is Python.
Code
Lets start with approaching one item (= (is)land). To achieve that
- We should iterate through the rows
- We should iterate through the items in a row
We surely will do something with the item itself, which we described in regards to the recursive function. We will get back to this as a next step, but this function will essentially decide whether we encountered an island, or not, so we can use it to count our islands.
Pseudo code
def main():
island counter variable = 0
iterate through rows
iterate through items in a row
island counter variable += call recursive function()
return island counter variable
It is very easy now to translate to Python
def count_islands(grid):
"""
Input: 2D matrix, each item is [x, y] -> row, col.
Output: number of islands, or 0 if found none.
Notes: island is denoted by 1, ocean by 0 islands is counted by continously
connected vertically or horizontically by '1's.
It's also preferred to check/mark the visited islands:
- eg. using the helper function - mark_islands().
"""
islands = 0
for row_num, row in enumerate(grid):
for col_num, item in enumerate(row):
islands += mark_islands(row_num, col_num, grid)
return islands
The recursive function
As we discussed, we shall begin with defining our base case, which we kind of already did in the Approach section, so lets express it in code:
a. ) As the recursive function's name - mark_islands - indicate, we will mark the visited (is)lands at some point (spoiler alert: right after the base case). Let's decide on #, and use it to check whether we've been at the certain (is)land or not.
grid[row_num][col_num] == '#'
b. ) Similarly very straightforward to check whether we reached the water:
grid[row_num][col_num] == 0
c. ) Good. Now let's think about "being off the grid". We have to cover edge cases around the first and last row, just like the first and last column. We can bundle this logic into a separate function:
def is_item_invalid(row_num, col_num, grid):
return
row_num < 0 or
row_num >= len(grid) or
col_num < 0 or
col_num >= len(grid[0])
Now we can take care of marking the visited (is)land:
grid[row_num][col_num] = '#'
We are so close! There's not so much left from now on, but to define the neighbour islands on which we will call the function itself again.
(Is)lands can be connected either horizontally or vertically (not diagonally) as per our task definition, which leaves us with four neighbours. For readability I decided to use dictionaries for each neighbours.
top_neighbor = {
'row': row_num + 1,
'col': col_num
}
bottom_neighbor = {
'row': row_num - 1,
'col': col_num
}
left_neighbor = {
'row': row_num,
'col': col_num - 1
}
right_neighbor = {
'row': row_num,
'col': col_num + 1
}
This standard format also makes possible to iterate through a neighbours list and call mark_islands on them.
neighbors = [
top_neighbor,
bottom_neighbor,
left_neighbor,
right_neighbor
]
for neighbor in neighbors:
mark_islands(neighbor['row'], neighbor['col'], grid)
return 1
Putting it all together
def is_item_invalid(row_num, col_num, grid):
return row_num < 0 or
row_num >= len(grid) or
col_num < 0 or
col_num >= len(grid[0])
def count_islands(grid):
"""
Input: 2D matrix, each item is [x, y] -> row, col.
Output: number of islands, or 0 if found none.
Notes: island is denoted by 1, ocean by 0 islands is counted by continously
connected vertically or horizontically by '1's.
It's also preferred to check/mark the visited islands:
- eg. using the helper function - mark_islands().
"""
for row_num, row in enumerate(grid):
for col_num, item in enumerate(row):
islands += mark_islands(row_num, col_num, grid)
return islands
def mark_islands(row_num, col_num, grid):
"""
Input: the row, column and grid
Output: None. Just mark the visisted islands as in-place operation.
"""
# base case
if is_item_invalid(row_num, col_num, grid) or grid[row_num][col_num] == '#' or grid[row_num][col_num] == 0:
return 0
# mark visited
grid[row_num][col_num] = '#'
top_neighbor = {
'row': row_num + 1,
'col': col_num
}
bottom_neighbor = {
'row': row_num - 1,
'col': col_num
}
left_neighbor = {
'row': row_num,
'col': col_num - 1
}
right_neighbor = {
'row': row_num,
'col': col_num + 1
}
neighbors = [
top_neighbor,
bottom_neighbor,
left_neighbor,
right_neighbor
]
for neighbor in neighbors:
mark_islands(neighbor['row'], neighbor['col'], grid)
return 1
squares = [[1, 1, 0, 1],
[1, 1, 0, 1],
[0, 0, 1, 1],
[1, 1, 1, 0]]
print(count_islands(squares))
Resources
[^1]: PyBites challenge: codechalleng.es/bites/263
[^2]: Medium article on recursion: medium.com/code-zen/recursion-demystified-2...